Download Adinkra.m

Click on the download link above. Save to your local machine by either

Right (control) clicking the above download link and saving to your local hard drive
or copying the raw text stored at the above link into a text editor and saving with only a .m extension.

Adinkra.m may be saved anywhere on your local machine and must then be installed as described in the “Installation Instructions” below.

Tutorials

Click here for various tutorials on how to use the functions of the Adinkra.m package summarized in the “About Adinkra.m” section below. The tutorials require installation of Adinkra.m as described below.

Installation Instructions

If updating Adinkra.m from a previous version, the old installation may first need to be deleted. Download and run DeleteAdinkra.nb before updating.

After downloading, install the Adinkra.m package with the File–>Install menu in Mathematica.

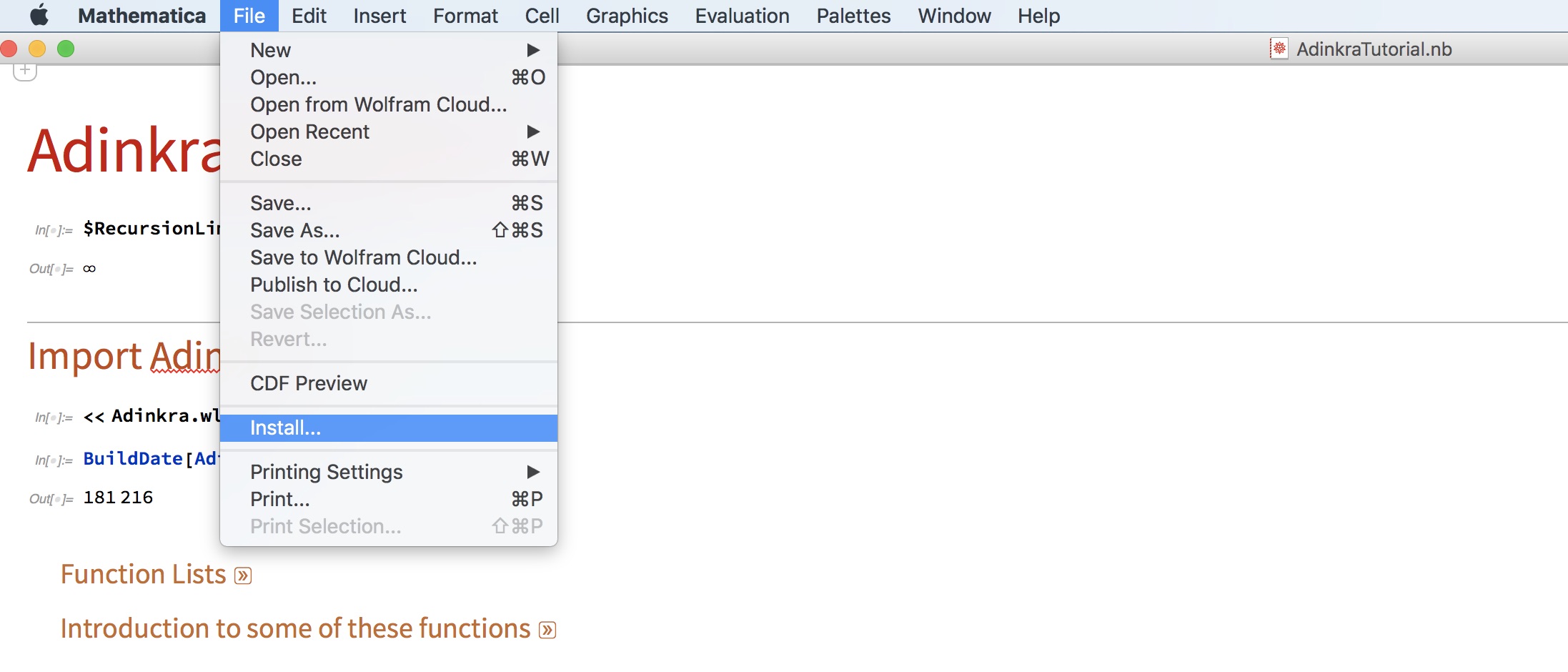
In the “Source” dropdown menu, select “From File…”

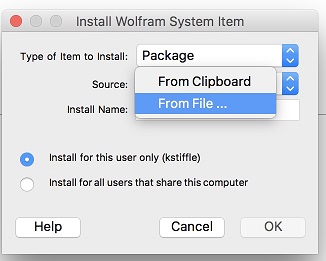
Navigate to where you downloaded “Adinkra.m” on you local machine, select it and click “ok”. Import the package into a notebook as follows:

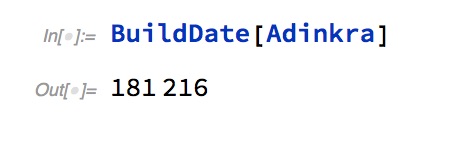
The date of the latest build, in yymmdd format, can be called by running, for example

About Adinkra.m

The Adinkra.m package includes tools to

Build 4D, N=1 SUSY transfromation laws in Majorana components
Reduce to 1D (0-brane reduction), generating L- and R-matrices for arbitrary d
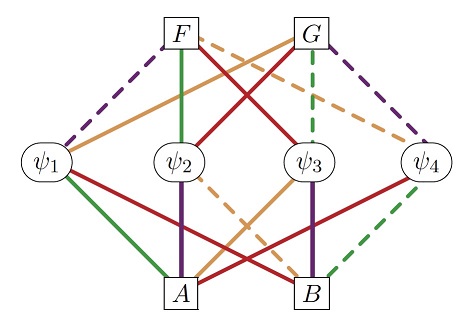
Graph L- and R- adinkra matrices as an adinkra for GR(4,4) matrices
Allows the user to encode their own arbitrary GR(d,N) L- and R- adinkra matrices and check that the GR(d,N) algebra is satisfied
Calculate chi_0 and holoraumy of adinkra matrices for arbitrary GR(d,N)
Print out L, R, holoraumy matrices and closure relationship in a GL(d/4) x GL(4) tensor product basis in symbolic form ready to be LaTexed by Mathematica's TeXForm command

The list of functions can be found by running

FunctionList[Adinkra]

which outputs the following:

SpaceTime:
IndexRange[SpaceTime][Index], Index = mu, a, or RaiseCode

coordinates, \[CapitalStigma][mu], \[Eta][mu,nu], Cmetric[[a,b]], 
InverseCmetric[[a,b]], UD[Field,\[CapitalStigma][mu]] , Lap[Field], 
UP, DOWN, RaiseSTIndex[Field,RaiseCode1,RaiseCode2,...,RaiseCoden], 
RaiseFermionIndex[Field]

****************************************************************************************
****************************************************************************************

GenerateLandR:
NColors[D,Phi,Psi], LTable[DColor,Phi,Psi], 
RTable[DColor,Phi,Psi],GenerateLandR[DColor,Phi,Psi,Rep]

****************************************************************************************
****************************************************************************************

AdinkraEssentials:
IndexRange[AdinkraEssentials][Index], Index = p1, II, ReportLevel, or 
pm

***IMPORTANT****: Default Settings are VScaleFactor = 
VtildeScaleFactor = -I, VsoNScaleFactor = -I/(2 VsoNScaleFactor), 
VtildesoNScaleFactor = -I/(2 VtildesoNScaleFactor)

Reports: AdinkraReport[Rep,ReportLevel], 
AdinkraPreliminaryReport[L,R], AdinkraPreliminaryReport[Rep], 
AdinkraPreliminaryReportO[Rep], AdinkraHoloMonoReport[Rep], 
AdinkraSummaryReport[Rep], AdinkraFullReport[Rep]

Basic Functions: nMatrices[Matrices], nRows[Matrices], 
nColumns[Matrices], Commute[Matrix1,Matrix2], NColors[Rep], 
NColors[L,R], dmin[N], dbosons[Rep], dbosons[L,R], dfermions[Rep], 
dfermions[L,R], WordW[{p1,p2,...,pN}]

Intense Calculations: Gadget[Rep1,Rep2], BosonGadget[Rep1,Rep2], 
ListOfIdenticalMonoOrHolo[MonoOrHolo,Rep], 
NumDistinctHoloOrMono[HoloOrMono,Rep]

Print Functions: PrintL[Rep][II], PrintR[Rep][II], 
PrintGALR[Rep][II,JJ], PrintGARL[Rep][II,JJ], PrintV[Rep][II,JJ], 
PrintVtilde[Rep][II,JJ], PrintZetaGen[Rep][II], 
PrintHoloraumy[Rep][{p1,p2,...,pN}], 
PrintMonodromy[Rep][{p1,p2,...,pN}],PrintZetatildeGen[Rep][II], 
PrintHoloraumytilde[Rep][{p1,p2,...,pN}], 
PrintMonodromytilde[Rep][{p1,p2,...,pN}], 
PrintVtildePM[pm][Rep][II,JJ], PrintVtildePM[pm][Rep][II,JJ], 
PrintAllL[Rep], PrintAllR[Rep], PrintAllGALR[Rep], PrintAllGARL[Rep], 
PrintAllV[Rep], PrintAllVtilde[Rep], PrintAllZetaGen[Rep], 
PrintAllHoloraumy[Rep], 
PrintAllMonodromy[Rep],PrintAllZetatildeGen[Rep], 
PrintAllHoloraumytilde[Rep], PrintAllMonodromytilde[Rep], 
PrintAllVtildePM[pm][Rep], PrintAllVtildePM[pm][Rep], 
,PrintSigmaProduct[Matrix], PrintLSigmaProduct[Rep], 
PrintRSigmaProduct[Rep]

Test Functions: CorrectDimensions[Rep], CorrectDimensions[L,R], 
TransposeTest[Rep], TransposeTest[L,R], InverseTest[Rep], 
InverseTest[L,R], RO[Rep], Chi0Report[L,R], GATest[Rep], GATest[L,R], 
soNTest[Matrices], su2Test[MgenPM[pm]][Rep], 
MutuallyCommuteTest[M1,M2], LinearlyIndependent[Mgen]

Data generated by GenerateAdinkraData[Rep], 
GenerateAdinkraData[Rep,Orthogonal], GenerateAdinkraDataO[Rep], 
GenerateAdinkraData[Rep,L], or GenerateAdinkraData[Rep,L,R]:
L[Rep], R[Rep], GALR[Rep], GARL[Rep], chi0[Rep], ncis[Rep], 
ntrans[Rep], V[Rep], Vtilde[Rep], VsoN[Rep], VtildesoN[Rep], 
ZetaGen[Rep], Holoraumy[Rep], Monodromy[Rep], ZetatildeGen[Rep], 
Holoraumytilde[Rep], Monodromytilde[Rep], VPM[pm][Rep], 
VtildePM[pm][Rep], VsoNPM[pm][Rep], VtildesoNPM[pm][Rep] 
cSoln[V[Rep]], cSoln[Vtilde[Rep]]

****************************************************************************************
****************************************************************************************

BasisDecomposition:
IndexRange[BasisDecomposition][Index], Index = mu, ahat, a, d, or n

General Matrix Tools:
sigma[mu], \[Alpha]matrix[ahat], \[Beta]matrix[ahat], 
SigmaProduct[mu1,mu2,...,mun], SigmaProductMF[mu1,mu2,...,mun], 
SigmaMatrixProduct[mu,AnyMatrix], \[Rho]matrix[mu,nu], 
\[Omega]matrix[n][a], Basis[d][a,mu,nu], TestOrthogonal\[Sigma], Test
\[Rho]Orthogonal, Test\[Omega]Orthogonal[n], TestBasisOrthogonal[d], 
Coeffs[d][Matrix][a,mu,nu]

GenerateCoeffs[Rep] generates adinkra representation specific 
functions:
LCoeffs[Rep][II], CheckLCoeffs[Rep], RCoeffs[Rep][II], 
CheckRCoeffs[Rep], VCoeffs[Rep][II,JJ], CheckVCoeffs[Rep], 
VtildeCoeffs[Rep][II,JJ], CheckVtildeCoeffs[Rep], 
VPMCoeffs[pm][Rep][II,JJ], CheckVPMCoeffs[pm][Rep], 
VtildePMCoeffs[pm][Rep][II,JJ], CheckVtildePMCoeffs[pm][Rep], 
NumberNonZero[LCoeffsMat], CoeffsSummaryReport[Rep], 
CoeffsFullReport[Rep_]

Print Functions:
 PrintSigmaProduct[Matrix], PrintBasis[Matrix], PrintLBasis[Rep][II], 
PrintRBasis[Rep][II], PrintGALRBasis[Rep][II,JJ], 
PrintGARLBasis[Rep][II,JJ], PrintVBasis[Rep][II,JJ], 
PrintVtildeBasis[Rep][II,JJ], PrintVPMBasis[pm][Rep][II,JJ], 
PrintVtildePMBasis[pm][Rep][II,JJ], PrintLSigmaProduct[Rep], 
PrintRSigmaProduct[Rep]

****************************************************************************************
****************************************************************************************

BC4Tools:

IndexRange[BC4Tools][Index], Index = n, a, [Mu], A, II, or tt

Functions: 
HPerm[a], H[[a]], S3Perm[\[Mu]], S3[[\[Mu]]], VierPerm[A], Vier[[A]], 
BC4[[n,a,\[Mu],A,II,JJ]] , BC4Perm[n,a,\[Mu],A][[II,JJ]], 
QuaternionTestIJK[Quat], QuaternionTestKJI[Quat], Digit[Num,Pow], 
ell[Rep][tt,a][II,JJ], kappa[Rep][ti,a][II,JJ], 
IellABColor[Rep][[a]], PrintIell[Rep][[a]], IellABCode[Rep][[a]], 
AntisymmetryCheck[Object1], BC4Color[n,a,\[Mu],A][L], 
BC4ColorPerm[n,a,\[Mu],A][L],BC4Boson[n,a,\[Mu],A][L],BC4BosonPerm[n,
a,\[Mu],A][L], 
HList,S3List,VierList,PrintBC4Perm[n,a,\[Mu],A],PrintBC4BosonPerm[n,a,
\[Mu],A],PrintBC4FermionPerm[n,a,\[Mu],A],PrintBC4ColorPerm[n,a,\[Mu],
A],L[Q],L[Qtilde],L[RepCode]

****************************************************************************************
****************************************************************************************

GraphingTools:
IndexRange[GraphingTools][list]

 AdinkraGreen, AdinkraViolet, AdinkraOrange, AdinkraRed, 
padLmatrix[L], adjacencyToEdge[mat,col], buildrules[list], Valise, 
GraphAdinkra[L], GraphAdinkra[L,BuildRules[list], 
ExportAdinkra[L,BuildRules[list],filename]

****************************************************************************************
****************************************************************************************

In the above list, the functions are organized in terms of the notebooks with which they are created. The FunctionList for each sub-notebook may be called independently. If for instance just a list of GraphingTools is desired, run

FunctionList[GraphingTools]